Booleska algebra. Del 2. Grundläggande lagar och funktioner

Fortsättning av berättelsen om booleska algebra, konventioner, regler, operationer. Övergång till grunderna i kontaktkretsar.

den första artikeln George Bull beskrivs som skaparen av logikens algebra. Den andra artikeln kommer att beskriva de grundläggande operationerna i booleska algebra och metoder för att förenkla booleska uttryck. Så Booleska algebra använder uttalanden som argument och inte deras betydelse, utan uttalandens sanning eller falska.

Formen för att skriva uttryck i booleska algebra.

Om uttalandet är sant, är det skrivet så här: A = 1, om det är falskt, då A = 0 (det är ju inte sant att potatisen är en frukt). För alla påståenden är A antingen sann (A = 1) eller falsk (A = 0). Det kan inte finnas någon mitt här. Vi har redan pratat om detta.

Om du ansluter två enkla uttalanden med facket Och får du ett komplext uttalande, som kallas en logisk produkt. Låt oss ta två enkla uttalanden: "Tre är mer än två" kommer vi att beteckna med bokstaven A, "Tre mindre än fem" - med bokstaven B.

Därför är det komplexa uttalandet "Tre är mer än två Och mindre än fem" logiskt (i detta fall med stor bokstaven Och säger att detta är en "OCH" logisk operation, såväl som senare i texten "ELLER" och "INTE.") och B. Det betecknas enligt följande: A ^ B eller A * B.

Logisk multiplikation (operation "OCH").

I elementär algebra A * A = A2. Men i Buhls algebra A * A = A2 = A, A * A = A, eftersom multiplikationstecknet (*) nu betyder ... Och ... i betydelsen av Och ... Och. All vår erfarenhet bekräftar att A&A är samma som A. ensam. Man kan inte hålla med om detta. Sanningen i uttalandet förändras inte om det upprepas av faktorn flera gånger.

Produkten från två påståenden anses vara sann (lika med 1), då, och endast om båda faktorerna är sanna och falska (lika med 0) om minst en av faktorerna är falska. Håller med om att dessa regler inte strider mot sunt förnuft, och dessutom uppfyller de fullständigt reglerna för elementär algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Den första jämlikheten lyder enligt följande: om både A och B är sanna, är produkten A * B sann. I Buhl-algebra ersätter multiplikationstecknet (*) unionen I.

Logiska produkter kan inte innehålla två, utan ett större antal uttalanden - faktorer. Och i detta fall är produkten sant endast när samtidigt alla uttalanden-faktorer är sanna.

Logiskt tillägg (ELLER operation)

Om två uttalanden är anslutna av en facklig organisation eller. den bildade sammansatta meningen kallas en logisk summa.

Tänk på ett exempel på en logisk summa. Att säga A: "Idag går jag på bio."

Uttalande B: "Idag ska jag åka till diskoteket." Vi lägger till båda uttalandena och får: "Idag ska jag gå på film ELLER till ett diskotek."

Detta komplexa uttalande betecknas på följande sätt: A + B = C eller (A VB) = C.

Med C betecknade vi ett komplext uttalande av en logisk summa.

I exemplet som behandlas kan fackföreningen OR inte användas i exklusiv mening. Samma dag kan du komma till biografen och till diskoteket. Och här är ordet:

”Ordföranden för trädgårdsskötselspartnerskapet kommer att vara Petrov eller Ivanov,” är inte en logisk summa, eftersom bara en person kommer att vara ordförande, och den andra kommer att vara en amatörs vanlig trädgårdsmästare.

Tecknet V för den logiska summan väljs eftersom det är den initiala bokstaven i det latinska ordet "vel", vilket betyder "eller", i motsats till det latinska ordet "aut>, vilket betyder" och ". Nu borde det vara klart för alla varför den logiska produkten indikeras av skylten ^.

I elementär algebra finns det en regel A + A = 2A. Denna regel är sant, oavsett vilket nummer som representeras av bokstaven A. I booleska algebra motsvarar regeln A + A = A den hela vår livserfarenhet säger att att säga A ELLER A eller båda A är bara en annan och längre väg att säga bara A.

Som alla sammansatta uttalanden kan summan av de två påståenden A och B vara sant eller falskt. Summan betraktas som sann, det vill säga lika med enhet, om åtminstone ett av termerna är sant:

A + B = 1 om OR A = 1 ELLER B = 1, vilket överensstämmer med konventionell aritmetik:

1+0 = 0+1 = 1.

Om båda summerade uttalanden är sanna, betraktas summan också som sann, därför har vi i den booleska algebra: (1) + (1) = 1.

Fästarna ställs in här för att betona villkoren, innebörden av detta tillägg och inte aritmetiska.

Summan av två påståenden anses vara falsk och lika med noll om, men endast om båda termerna är falska. Härifrån:

0 + 0=0.

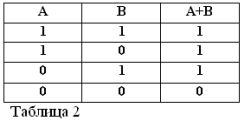
Så summan av de två uttalandena A + B anses vara sant om det är sant, ELLER A, ELLER B, ELLER båda uttrycker tillsammans. Således betecknas ordet OR med +.

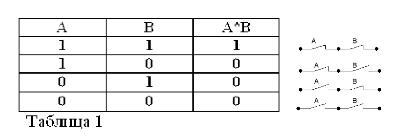
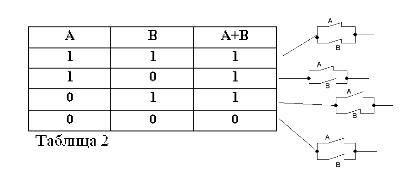
Kom ihåg att påståenden A och B endast kan vara sanna eller falska och därför har ett mått på sanning 1 eller 0, kan resultaten av de övervägda OCH- och ELLER-operationerna sammanfattas i tabellerna 1 och 2.

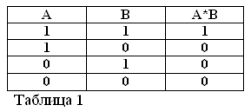
Den tredje operationen, som används allmänt av Buhl algebra, är negationsoperationen - INTE. Vi påminner dig om att elementär algebra använder operationerna ADD, D Subtract, Multiply by, Divide by och några andra.

För varje uttalande A finns det dess negation INTE A, som vi kommer att beteckna med symbolen / A. Detta borde inte vara i tvivel.

Vi ger exempel: "Vi kommer till skogen" A, "Vi kommer inte till skogen" / A.

Om påståendet A är sant, det vill säga A = 1, måste dess negation / A vara falsk / A = 0. Och vice versa, om något uttalande är falskt, så är dess negation sant. Till exempel: "En häst äter inte hö" / A = 0, "En häst äter inte hö" (A = 1). Detta kan uttryckas i tabell 3.

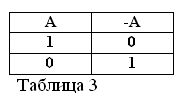
Att fastställa betydelsen av handlingen av negation, och antaga att av de två påståendena A och / A alltid är en sann, följer två nya formler i den booleska algebra:

A + (/ A) = 1 och A * (/ A) = 0.

Det finns också andra formler som förenklar den logiska behandlingen av uttalanden. Till exempel 1 + A = 1, eftersom summan, enligt definitionen av tillägg, i fallet när en term är lika med enhet, summan alltid är lika med enhet. Resultatet beror inte på om A = 0 eller A = 1.

Var och en av de tre logiska operationerna som vi undersökte (OCH, ELLER, INTE) har vissa egenskaper som ligger nära reglerna för elementär algebra. Om alla är formulerade får vi 25 regler för boolesisk algebra. De är tillräckligt för att lösa nästan alla logiska problem. Utan dessa regler blir det ganska svårt att lösa logiska problem på grund av deras uppenbara komplexitet. Att försöka hitta rätt svar utan att använda reglerna betyder att byta ut dem med uppfinningsrikedom och allmän resonemang. Regler underlättar detta arbete kraftigt och sparar tid.

Inom ramen för artikeln är det omöjligt att ta hänsyn till alla dessa 25 regler, men de som önskar kan alltid hitta dem i relevant litteratur.

Som redan nämnts i den första artikeln 1938 använder den unga amerikanska forskaren Claude Shannon i sin artikel "Symbolisk analys av relä- och kopplingskretsar" för första gången Booles algebra för reläteknologiproblem. Shannons upptäckt var att han insåg att metoden för att designa relämaskiner och elektroniska datorer faktiskt är en gren av matematisk logik.

Det händer ofta. Under många år har forskaren arbetat med ett problem som verkar helt onödigt för hans landsmän - bara kul. Men decennier och ibland århundraden går, och en teori som ingen behöver förvärvar inte bara rätten att existera utan utan ytterligare framsteg blir otänkbara.

Vad hjälpte Shannon andra gången att "upptäcka" booleska algebra? Fallet? Inget sådant.

Kärleken till relämaskiner, byggda på konventionella omkopplare och reläer, hjälpte den unga forskaren att ansluta en glömd teori med uppgifterna i automatiska telefonväxlar, som han arbetade på den tiden. Senare introducerade Shannon samma idé om ”ja eller nej” i diskreta meddelanden och lägger grunden för en hel del av cybernetik - informationsteori.

Buhls algebra var mycket lämplig för analys och syntes av reläkretsar. Det räckte med att acceptera som ett riktigt uttalande: "Det finns en signal i kretsen", och som en falsk - "Det finns ingen signal i kretsen", som en ny algebra dök upp - signalalgebra, reläkretsalgebra.

Den nya algebra gäller endast för övervägande av relä- och kopplingskretsar. När allt kommer omkring är det bara i sådana scheman uppfyllda villkoret "det finns en signal" och "ingen signal". Då signalen ändras kontinuerligt och förvärvar ett godtyckligt stort antal mellanliggande förhållanden (en sådan signal kallas analog), är reläalgebra inte tillämplig. Detta måste alltid komma ihåg. Men bara majoriteten av elektroniska datorer och cybernetiska maskiner använder den diskreta principen för signalbehandling, som är baserad på elementen "ja - nej".

Uttrycket "Kontakt stängd" accepterades av Shannon som sant (1) och "Kontakt öppen" som falsk (0). Resten av "algebra", inklusive operationerna AND, OR och NOT och 25 regler, lånade Shannon från Boole.

Reläkretsalgebra visade sig vara enklare än den booleska algebra, eftersom den endast handlar om element av typen "ja - nej". Dessutom är den nya algebra mer uppenbar.

Elementen i denna algebra är kontakterna, som vi kommer att beteckna med bokstäverna A, B, C ... Kontakten är stängd - A, kontakten är öppen - / A (bokstav med bindestreck).

Notationen är som ni ser helt från Booles algebra. En öppen kontakt är en negation av en sluten kontakt. Samma kontakt kan inte vara både stängd och öppen.

Låt oss komma överens om att om två kontakter i någon krets betecknas med samma bokstav betyder det att de alltid tar samma värden.

Vid varje givet ögonblick är de antingen båda öppna samtidigt eller så är båda stängda. Det enklaste sättet att föreställa sig mekaniskt anslutna tillsammans så att båda samtidigt öppnar eller stänger.

Om en kontakt i någon kedja är en negation av en annan kontakt, är deras betydelse alltid motsatta. Till exempel kan kontakterna C och / C aldrig vara öppna eller stängda samtidigt. Och i diagrammet kan de representeras mekaniskt anslutna: om en av dem öppnar, stänger den andra.

Vi börjar bekanta oss med reläalgebra genom att analysera de enklaste kretsarna som motsvarar OCH-, ELLER- och INTE-operationerna.

Produkten från två kontakter (drift OCH) är den krets som erhålls som ett resultat av deras seriekoppling: den är stängd (lika med 1) endast när båda kontakterna är stängda (lika med 1).

Summan av två kontakter (ELLER operation) kommer att vara kretsen som bildas när de är parallellt anslutna: den är stängd (lika med 1) när minst en av kontakterna som bildar kretsen är stängd (lika med 1).

Det motsatta av denna kontakt (operation INTE) är en kontakt som är lika med 0 (öppen) om denna kontakt är 1 (stängd) och vice versa.

Liksom i den booleska algebra, om kontakterna är betecknade med bokstäverna A och B, kommer vi att beteckna produkten av två kontakter med A * B, summan med A + B och kontakten mittemot A, av / A. Ovanstående förklaras i figurerna 1, 2 och 3.

Giltighet för tabeller som motsvarar AND, OR eller NOT operationer. nu borde ingen vara i tvivel.

Låt oss tänka på två exempel: 1 * 0 = 0 och 1 + 0 = 1.

Det framgår av figuren att en permanent stängd kontakt ansluten i serie med en ständigt öppen kontakt motsvarar en permanent öppen kontakt (1 * 0 = 0) En permanent stängd kontakt ansluten parallellt med en ständigt öppen kontakt motsvarar en permanent stängd kontakt.

När du har blivit bekant med kontaktkretsarnas aritmetik kan du beskriva alla reläkretsar med en formel med de accepterade konventionerna. I cybernetik kallas sådana formler strukturella.

Om strukturformeln för någon reläkrets är 1 kan en signal passera genom den - kretsen är stängd. Omvänt, om strukturens formel för kretsen är 0, kommer signalen inte att passera genom den - kretsen är trasig.Slutsats: två reläkretsar motsvarar varandra när deras strukturella formler är lika.

I fortsättningen av artikeln kommer vi att ta hänsyn till exempel på kontaktkretsar, typiska kontaktkretsar och deras ekvivalenter, samt att utarbeta diagram enligt strukturella formler. Vi tar också hänsyn till de viktigaste logiska kretsarna som utför funktionerna i den booleska algebra.

Fortsättning av artikeln: Booleska algebra. Del 3. Kontaktplaner

Boris Aladyshkin