Боолеова алгебра. Део 2. Основни закони и функције

Наставак приче о буловој алгебри, конвенцијама, правилима, операцијама. Прелаз на основе контактних кола.

Ин први чланак Георге Булл је описан као творац логичке алгебре. У другом чланку ће се описати основне операције боолеове алгебре и методе за поједностављивање логичких израза. Дакле, Боолова алгебра користи изјаве као аргументе, и не њихово значење, већ истину или неистинитост изјаве.

Образац за писање израза у бооле алгебри.

Ако је изјава тачна, онда се пише овако: А = 1, ако је лажна, онда је А = 0 (уосталом, није тачно да је кромпир плод). За било коју изјаву, А је или тачно (А = 1) или лажно (А = 0). Овдје не може бити средина. О томе смо већ разговарали.

Ако повежете две једноставне изјаве са унијом И, добићете сложену изјаву која се зове логички производ. Узмимо две једноставне изјаве: „Три су више од две“ означићемо словом А, „Три мање од пет“ - словом Б.

Отуда је сложена изрека „Три је више од две А мање од пет“ логична (у овом случају велика слова И означава да је то логичка операција „И“, као и касније у тексту „ИЛИ“ и „НЕ“). и Б. Означен је на следећи начин: А ^ Б или А * Б.

Логичко множење (операција „И“).

У елементарној алгебри А * А = А2. Али у Буховој алгебри А * А = А2 = А, А * А = А јер знак множења (*) сада значи ... И ... у смислу Анд ... И. Све наше искуство потврђује да је А&А исто што и А. Само се не могу сложити са тим. Истина изјаве не мења се ако је фактор више пута поновио.

Продукт две изјаве сматра се истинитим (једнаким 1), тада и само ако су оба фактора тачна, и лажним (једнаким 0) ако је бар један од фактора лажан. Слажете се да ова правила нису у супротности са здравим разумом и, поред тога, у потпуности су у складу са правилима елементарне алгебре:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Прва једнакост гласи како слиједи: ако су и А и Б тачне, тада је производ А * Б тачан. У Бухл алгебри знак множења (*) замењује сједињење И.

Логични производи могу укључивати не два, већ већи број изјава - фактора. И у овом случају, производ је истинит само када су истовремено истините све изјаве-фактори.

Логички додатак (ИЛИ рад)

Ако су две изјаве повезане синдикатом ИЛИ. да се формирана сложена реченица назива логичким збројем.

Размотрите пример логичке суме. Рећи А: "Данас ћу ићи у биоскоп."

Изјава Б: „Данас ћу ићи у диско.“ Додајемо обе изјаве и добили смо: „Данас ћу ићи у биоскопе или у дискотеку“.

Ова сложена изјава је означена на следећи начин: А + Б = Ц или (А В Б) = Ц.

Ц смо означили сложеном изјавом логичке суме.

У примјеру који се разматра, унија ИЛИ се не може користити у ексклузивном смислу. Заиста, истог дана можете доћи у биоскоп и диско. А ево изреке:

„Председавајући вртларског партнерства биће Петров или Иванов“, није логична сума, јер ће само једна особа бити председник, а друга аматерски обични баштован.

Знак В за логички збир је изабран, јер је почетно слово латинске речи "вел", што значи "или", за разлику од латинске речи "аут>, што значи" и ". Сада би свима требало бити јасно зашто је логички производ означен знаком ^.

У елементарној алгебри постоји правило А + А = 2А. Ово правило је тачно, без обзира на то који је број представљен словом А. У буловој алгебри њему одговара правило А + А = А. Све наше животно искуство каже да рећи А ИЛИ А или оба А је само још један и дужи начин да кажеш само А.

Као и свака сложена изјава, збир две изјаве А и Б може бити тачан или лажан. Збир се сматра тачном, то јест једнаком јединству, ако је бар један од тачака:

А + Б = 1 ако је ОР А = 1 ИЛИ Б = 1, што је у складу са уобичајеном аритметиком:

1+0 = 0+1 = 1.

Ако су обе збројене изјаве тачне, тада се и збир сматра тачним, па у боовој алгебри имамо: (1) + (1) = 1.

Овде су заграде постављене како би се нагласило условно, значење овог додатка, а не аритметика.

Збир две изјаве сматра се лажним и једнак је нули ако, али само ако су оба термина лажна. Одавде:

0 + 0=0.

Дакле, зброј две изјаве А + Б сматра се истинитим ако је тачно, ИЛИ А, ИЛИ Б, ИЛИ оба термина заједно. Дакле, реч ИЛИ је означена са +.

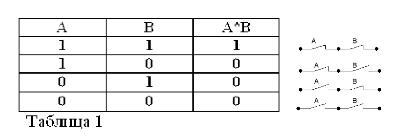
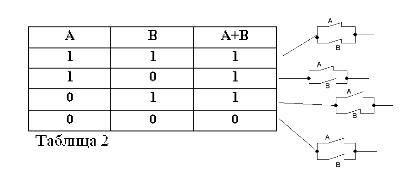
Сјећајући се да изјаве А и Б могу бити само истините или лажне и, према томе, имају мјеру истине 1 или 0, резултати разматраних АНД и ОР операција могу се сажети у табеле 1 и 2.

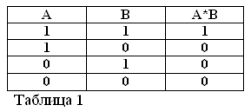
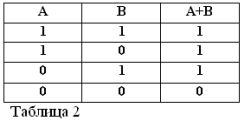
Трећа операција коју Бухл алгебра широко користи је негација - НЕ. Подсећамо вас да се основна алгебра користи операцијама АДД, Д одузимањем, множењем, дељењем и неким другима.

За сваку изјаву А постоји негација НЕ А, коју ћемо означити с / А. Ово не би требало да буде у сумњи.

Дајемо примере: „Ићи ћемо у шуму“ А, „Нећемо у шуму“ / А.

Ако је изјава А тачна, то јест А = 1, онда њена негација / А мора бити лажна / А = 0. И обрнуто, ако је нека изјава лажна, онда је њена негација тачна. На пример: „Коњ не једе сено“ / А = 0, „Коњ не једе сено“ (А = 1). То се може изразити у табели 3.

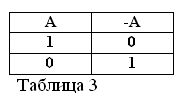
Одређивање значења акције негације и претпостављање да је од две изјаве А и / А увек једна истина, следе две нове формуле боолове алгебре:

А + (/ А) = 1 и А * (/ А) = 0.

Постоје и друге формуле које поједностављују логичку обраду изјава. На пример, 1 + А = 1, јер је према дефиницији сабирања, у случају када је један израз једнак, сума увек једнака јединици. Добивени резултат не зависи од тога да ли је А = 0 или А = 1.

Свака од три логичке операције које смо испитивали (И, ИЛИ, НЕ) има одређена својства која су блиска правилима елементарне алгебре. Ако су сви формулисани, онда ћемо добити 25 правила боолове алгебре. Сасвим су довољни да реше готово сваки логички проблем. Без ових правила постаје прилично тешко решити логичке проблеме због њихове привидне сложености. Покушај да нађете тачан одговор без употребе правила значи да их замените домишљатошћу и општим резоновањем. Правила увелико олакшавају овај рад и штеде време.

У оквиру чланка немогуће је размотрити свих ових 25 правила, али они који то желе могу их увек наћи у релевантној литератури.

Као што је већ споменуто у првом чланку 1938. године, млади амерички научник Цлауде Сханнон, у свом чланку „Симболичка анализа релејних и комутацијских кругова“, први пут користи боолеову алгебру за проблеме релејне технологије. Сханноново откриће је да је схватио да је метода дизајнирања релејних машина и електронских рачунара заправо грана математичке логике.

То се често дешава. Већ годинама научник ради на проблему који својим сународницима делује потпуно непотребно - само забави. Али пролазе деценије, а понекад и векови, а теорија која никоме није потребна не само да стиче право на постојање, већ и без тога даљи напредак постаје незамислив.

Шта је помогло Сханнону да други пут "открије" Боолеове алгебре? Случај? Ништа слично.

Љубав према релејним машинама, изграђеним на конвенционалним прекидачима и релејима, помогла је младом научнику да повеже заборављену теорију са задацима аутоматских телефонских централа, на којима је у то време радио. Касније је Сханнон исту идеју „да или не“ увео у дискретне поруке и поставио темеље читавом делу кибернетике - теорије информација.

Бухлова алгебра била је веома погодна за анализу и синтезу релејних кола. Било је довољно да прихватимо као истиниту изјаву: „У кругу постоји сигнал“, а као лажна - „Нема сигнала у кругу“, како се појавила нова алгебра - сигнална алгебра, алгебра релејног кола.

Нова алгебра важи само за разматрање релејних и преклопних кола. На крају крајева, само у таквим схемама је испуњено стање „постоји сигнал“ и „нема сигнала“. Тамо где се сигнал непрекидно мења, добијајући произвољно велики број интермедијарних услова (такав се сигнал назива аналогни), релативна алгебра није применљива. То се увек мора имати на уму. Али само већина електронских рачунара и кибернетичких машина користи дискретни принцип обраде сигнала, који се заснива на елементима „да - не“.

Израз "Контакт затворен" Сханнон је прихватио као истинит (1), а "Контакт отворен" као лажан (0). Остатак "алгебре", укључујући операције АНД, ОР, НОТ и 25 правила, Сханнон је позајмила од Бооле-а.

Алгебра релејног круга показала се једноставнијом од Боолове алгебре јер се бави само елементима типа "да - не". Поред тога, нова алгебра је визуелније.

Елементи у овој алгебри су контакти, које ћемо означити словима А, Б, Ц ... Контакт је затворен - А, контакт је отворен - / А (слово са цртицом).

Нотација је, као што видите, потпуно преузета из боолове алгебре. Отворени контакт је негација затвореног контакта. Исти контакт не може бити ни затворен ни отворен.

Слажемо се да ако су у било којем кругу два контакта означена истим словом, то значи да увек узимају исте вредности.

У било којем тренутку су или истовремено отворене или су затворене. Најлакши начин да их замислите механички повезани заједно, тако да се обоје истовремено отварају или затварају.

Ако је у неком ланцу контакт негација другог контакта, њихова значења су увек супротна. На пример, контакти Ц и / Ц никада не могу бити истовремено отворени или истовремено затворени. И на дијаграму се могу представити механички повезани: ако се један од њих отвори, онда се други затвара.

Своје упознавање са релејском алгебром започињемо анализом најједноставнијих кола која одговарају операцијама АНД, ОР и НОТ.

Производ два контакта (рад И) је склоп добијен као резултат њихове серијске везе: он је затворен (једнак 1) само када су оба контакта затворена (једнака 1).

Зброј два контакта (ИЛИ рад) ће бити склоп који се формира када су паралелно повезани: он је затворен (једнак 1) када је бар један од контаката који творе склоп затворен (једнак 1).

Супротност овом контакту (операција НЕ) је контакт једнак 0 (отворен) ако је контакт 1 (затворен), и обрнуто.

Као и код Боолове алгебре, ако су контакти означени словима А и Б, тада ћемо продукт два контакта означити са А * Б, зброј са А + Б, а контакт насупрот А, са / А. Наведено је објашњено на сликама 1, 2 и 3.

Важност табела које одговарају операцијама АНД, ОР и НОТ. сада нико не би требао бити у недоумици.

Зауставимо се на два примера: 1 * 0 = 0 и 1 + 0 = 1.

Из слике се види да је трајно затворени контакт повезан низом са стално отвореним контактом еквивалентно трајно отвореном контакту (1 * 0 = 0) Трајно затворени контакт повезан паралелно са стално отвореним контактом еквивалентан је трајно затвореном контакту.

Упознавши се са аритметиком контактних кругова, можете описати било који релејни круг формулом помоћу прихваћених конвенција. У кибернетици се такве формуле називају структуралним.

Ако је структурна формула било ког релејног круга 1, тада сигнал може проћи кроз њега - круг је затворен. Супротно томе, ако је структурална формула круга 0, сигнал неће проћи кроз њу - круг је прекинут.Закључак: два релејна круга једнака су једнаком другом када су њихове структурне формуле једнаке.

У наставку чланка размотрићемо примере контактних кола, типичних контактних кола и њихових еквивалената, као и цртање дијаграма према структурним формулама. Такођер разматрамо главна логичка кола која обављају функције Боолове алгебре.

Наставак чланка: Боолеова алгебра. Део 3. Шеме контаката

Борис Аладисхкин