категории: Препоръчани статии » Практическа електроника
Брой преглеждания: 32001
Коментари към статията: 2
Кондензатори в електронни схеми
 В предишните статии накратко говорихме за работата на кондензаторите в променливотокови вериги, как и защо кондензаторите преминават променлив ток (виж - AC кондензатори). В този случай кондензаторите не се нагряват, мощността не им се разпределя: в едната половина на вълната на синусоида кондензаторът се зарежда, а в другия, той естествено се разтоварва, докато прехвърля запаметената енергия обратно към източника на ток.
В предишните статии накратко говорихме за работата на кондензаторите в променливотокови вериги, как и защо кондензаторите преминават променлив ток (виж - AC кондензатори). В този случай кондензаторите не се нагряват, мощността не им се разпределя: в едната половина на вълната на синусоида кондензаторът се зарежда, а в другия, той естествено се разтоварва, докато прехвърля запаметената енергия обратно към източника на ток.
Този метод на преминаващ ток ви позволява да наречете кондензатора свободно съпротивление и затова кондензаторът, свързан към изхода, не прави брояча на въртене. И всичко това е така, защото токът в кондензатора изпреварва точно 1/4 от времето, приложено към него напрежението.
Но този фазов аванс дава възможност не само да „измами“ брояча, но също така дава възможност за създаване на различни схеми, например генератори на синусоидални и правоъгълни сигнали, закъснения във времето и различни честотни филтри.
В процеса на тази история ще е необходимо понякога да си припомняме казаното вече, така да се каже, да обобщим. Това ще помогне да не се върнете към предишни статии, за да си припомним проста формула или просто „какво е това?“
Паралелно и серийно свързване на кондензатори
При паралелно свързване на кондензатори общият капацитет е просто аритметичната сума на капацитетите. Естествено, с това включване общият капацитет ще бъде по-голям от капацитета на най-големия кондензатор. Ctotal = C1 + C2 + C3 + ... + Cn.
В случай на серийна връзка, общият капацитет е по-малък от този на най-малкия.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Когато два еднакви кондензатора са свързани последователно, общият капацитет ще бъде равен на половината от капацитета на един: например, когато свързвате два кондензатора по 1 µF всеки, общият капацитет ще бъде 0,5 µF.
Капацитет Xc
Тук всичко, както при свързването на резистори, е само обратното: серийна връзка намалява общия капацитет, докато паралелна го увеличава. Това обстоятелство не трябва да се забравя при свързване на кондензатори, тъй като увеличаването на капацитета води до намаляване на капацитета Xc
Xc = 1/2 * π * f * C.
От гледна точка на математиката това е съвсем естествено, защото капацитетът C е в знаменателя на дроби. Между другото, честотата f е на едно и също място, така че увеличаването на честотата също води до намаляване на капацитета Xc. Физическият смисъл на това е, че чрез един и същ кондензатор е по-добре, по-безпрепятствено, да преминават високи честоти. Това ще бъде обсъдено малко по-късно, когато става въпрос за нискочестотни и високочестотни филтри.
Ако вземем кондензатор с капацитет 1 μF, тогава за честота от 60 Hz неговият Xc ще бъде 2653 ома, а за честота 400 Hz същият кондензатор има Xc само 398 ома. Желаещите могат да проверят тези резултати по формулата, замествайки π = 3.14, честотата в херца и капацитета във фаради. Тогава резултатът ще бъде в оми. Всичко трябва да отговаря на системата SI!
Но кондензаторите се използват не само като устойчивост на амортисьори за свободно амортизиране или в токоизправителни филтри. Без тяхното участие, вериги за генератори с ниска и висока честота, различни преобразуватели на вълни, диференциращи и интегриращи вериги, усилватели и други схеми.
След това ще бъдат разгледани различни електрически сигнали, с които кондензаторите трябва да работят. На първо място, това са периодични сигнали, подходящи за наблюдение с осцилоскоп.
Период и честота на трептенията
Следователно периодично трептене се нарича периодично, което без прекъсване повтаря същата форма, например едно синусоидално трептене. Продължителността на този пълен размах се нарича точно период Т и се измерва в секунди, милисекунди, микросекунди.Съвременната електроника дори се занимава с наносекунди (милиардна част от секундата).
Броят периоди в секунда се нарича честотата (колко често) на трептенията f и се изразява в херц. 1Hz е честотата, с която се извършва едно колебание, един пълен период за 1 секунда. Съотношението на периода и честотата се изразява с простата формула T = 1 / f.
Съответно, знаейки периода на трептене, е много просто да се изчисли честотата f = 1 / T.
Ето как се изчислява честотата при измерване с осцилоскоп: броят клетки в даден период се изчислява, умножен по продължителността на една клетка, и периодът се получава, например, в микросекунди. И за да разберат честотата, те просто използваха последната формула.
обикновен електронен осцилоскоп Позволява ви да наблюдавате само периодични сигнали, които могат да се синхронизират с честотата на почистване, за да получите неподвижно изображение, подходящо за изследване. Ако изпратите сигнал до музикална програма до входа на осцилоскопа, няма да можете да спрете изображението за нищо. За наблюдение на такива сигнали се използват осцилоскопи за съхранение.
Когато периодът се измерва в милисекунди, честотата се получава в килогерц, за период, измерен в микросекунди, честотата вече се изразява в мегагерци. Това е, ако не спазвате изискванията на системата SI: период в секунди, честота в херца.
Несинусоидални вибрации
Както бе споменато по-рано, синусоида е най-често срещаната и подходяща за изследване и практическо използване на периодичната крива. В промишлени условия той се получава с помощта на електрически генератори, например, в водноелектрически централи. В електронните устройства се използват вибрации от най-различни форми.
По принцип това са три форми: синусоидална, правоъгълна и триъгълна, както е показано на фигура 1. И токът, и напрежението могат да имат такава форма, следователно фигурата показва само часовата ос, оста на ординатата е оставена без име.
Такива трептения се генерират от специални електронни вериги. Правоъгълните и триъгълните сигнали често се наричат импулсни. Съществуват обаче много електронни схеми, които извършват преобразуване на сигнала: например правоъгълник, триъгълник може да се направи от синусоида.
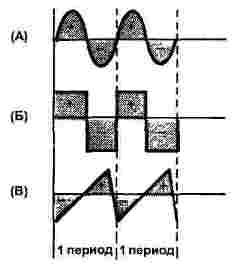
Фигура 1
И за трите сигнала фигурата показва два периода, всички сигнали имат еднаква честота.
Спектър на несинусоидални сигнали
Всеки електрически сигнал може да бъде представен като измерване на амплитудата в даден момент от време. Честотата на тези проби се нарича честота на дискретизация и най-малко два пъти по-висока от горната честота на измерения сигнал. След това от тези проби можете да възстановите оригиналния сигнал. Този метод се използва например при цифрово записване на звук. Този метод се нарича още анализ на времето.
Друг метод предполага, че всеки сигнал, дори правоъгълен, може да бъде представен като алгебраична сума от синусоиди с различни честоти и фази. Този метод се нарича честотен анализ. Но казаното „с различни честоти” не е напълно вярно: съставните синусоиди се наричат хармоници и честотите им се подчиняват на определени закони.
Синусоида, чиято честота е равна на честотата на квадратна вълна, се нарича основна или първа хармонична. Дори и хармониците се получават чрез умножаване на основната честота по четно число, а нечетни хармоници, съответно, по нечетни.
По този начин, ако първата хармоника има честота 1000 Hz, то втората е 2000 Hz, четвъртата е 4000 Hz и т.н. Странните хармоници ще имат честоти 3000Hz, 5000Hz. Освен това всяка хармоника е по-малка по амплитуда от основната: колкото по-висока е хармоничната, толкова по-малка е амплитудата.
В музиката хармониците се наричат обертонове. Именно те формират тембъра на звука, правят възможно разграничаването на цигулката от пианото, а китарата - от саксофона. Те не позволяват да объркат мъжкия и женския глас или да различават Петров от Иванов. И само самия синусоид вече не може да бъде разложен или сглобен от никакви сигнали.
Фигура 2 показва конструкцията на правоъгълен импулс.
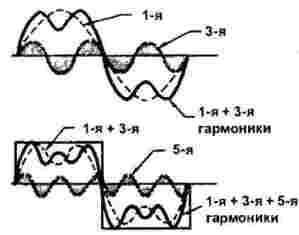
Фигура 2
Първата и третата хармоника са показани в горната част на фигурата. Лесно е да се види, че в един период от първата хармоника три периода на третия проход. В този случай амплитудата на третия хармоник е една трета от първата. Сумата от първата и третата хармоника също е показана тук.
По-долу, заедно със сумата от 1 и 3 хармоника, са показани още 5 хармоници: за период на правоъгълен сигнал той успява да направи точно пет периода. В този случай амплитудата му е още по-малка, по-точно, точно 1/5 от основната (първата). Но не бива да се мисли, че всичко завършва на петата хармоника: просто не може да бъде показано на фигурата, всъщност има много повече.
Образуването на триъгълни и триъгълни сигнали, показано на фигура 3, е малко по-сложно. Ако в предишния случай са участвали само нечетни хармоници, тогава дори хармоници влизат в игра.
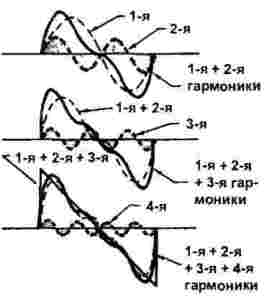
Фигура 3
По този начин можем да заявим факта, че с помощта на много хармоници се синтезира сигнал от всякаква форма, а броят и видът на хармониците зависят от формата на вълната, както е показано на фигури 2 и 3.
При ремонт и настройка на електронно оборудване се използва осцилоскоп за изучаване на електрически сигнали. Тя ви позволява да разгледате формата на периодичните сигнали, тяхната амплитуда, да измервате периода на повторение. Но хармониците, показани на фигури 2 и 3, не могат да се видят.
Дори ако свържете например електрическа китара с осцилоскоп, издърпате една струна, на екрана се появява синусоид, това е първата хармоника. В този случай не може да се говори за никакви обертонове. Същият синусоид ще се получи, ако духате в тръбата или флейта пред микрофона.
Как да получите правоъгълни импулси
След като се запознахме с електрическите сигнали, трябва да си припомним кондензаторите, с които е започнала статията. На първо място, трябва да се запознаете с една от класическите схеми на електрониката - мултивибратор, (Фигура 4) именно той генерира правоъгълни импулси. Веригата е толкова класическа, че започва да работи веднага, без да изисква никакви настройки или настройки.
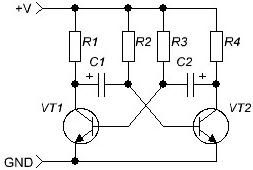
Фигура 4
Мултивибраторът е двустепенен усилвател, обхванат от положителна обратна връзка. Ако резисторите за натоварване на колектора R1 = R4, базовите резистори R2 = R3 и кондензаторите C1 = C2 са равни, мултивибраторът се нарича симетричен и генерира квадратни вълнови импулси от типа меандър - продължителността на импулса е равна на продължителността на паузата.
Работният цикъл на такива импулси (съотношението между периода и продължителността на импулса) е равен на два. В англоезичните схеми всичко е точно обратното: наричат го дежурен цикъл. Изчислява се като съотношението на продължителността на импулса към периода на неговата последователност и се изразява като процент. Така за меандъра работният цикъл е 50%.
Правилен ли е компютърът?
Името мултивибратор е предложено от холандския физик ван дер Пол, тъй като спектърът на правоъгълен сигнал съдържа много хармоници. Можете да проверите това, ако можете да поставите радиоприемник, работещ в средно вълнен диапазон, в близост до мултивибратор, който работи дори на звукова честота: виене ще дойде от високоговорителя. Това предполага, че освен звукова честота, мултивибраторът излъчва и високочестотни трептения.
За да се определи честотата на генериране, може да се използва формулата f = 700 / (C1 * R2).
При тази форма на формулата, капацитетът на кондензатора в микрофаради (μF), съпротивлението в кило-оми (KΩ), резултата в херц (Hz). По този начин честотата се определя от времевата константа на веригата C1 * R2; натоварванията на колектора не влияят на честотата. Ако вземем C1 = 0,02 μF, R2 = 39 KΩ, тогава получаваме f = 700 / (0,02 * 39) = 897,4 Hz.
Мултивибратор във възрастта на компютрите и микроконтролери Според тази схема тя почти никога не се използва, въпреки че може да е подходяща за различни експерименти. На първо място, с помощта на компютри. Ето как изглежда многовибраторната верига, сглобена в програмата Multisim. Връзката на осцилоскопа също е показана тук.
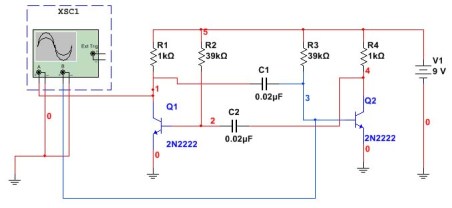
Фигура 5
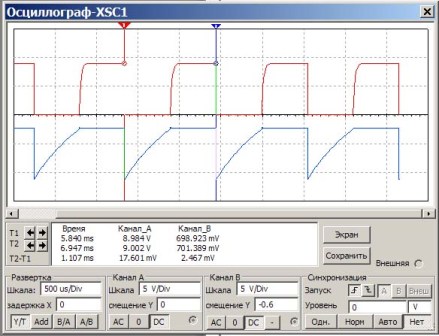
В тази схема се инсталират кондензатори и резистори, както в предишния пример. Задачата е да се провери изчислението по формулата дали ще бъде получена една и съща честота. За целта измерете периода на импулсите и след това ги преизчислете по честота. Резултатът от осцилоскопа Multisim е показан на фигура 6.
Фигура 6
Някои пояснения към фигура 6.
На екрана на осцилоскопа червеният импулс показва импулсите на колектора на транзистора, а синият - върху основите. Под екрана в голям бял прозорец числата показват резултатите от измерванията. Интересуваме се от графа „Време“. Времето се измерва с индикатори T1 и T2 (червени и сини триъгълници над екрана).
По този начин периодът на повторение на импулса T2-T1 = 1.107ms е показан доста точно. Остава само да се изчисли честотата f = 1 / T = 1 / 1.107 * 1000 = 903Hz.
Резултатът е почти същият като при изчисляването по формулата, която е дадена малко по-високо.
Кондензаторите могат да се използват не само отделно: в комбинация с резистори те ви позволяват просто да създавате различни филтри или да създавате вериги с фазово изместване. Но това ще бъде разгледано в следващата статия.
Продължение на статията: Кондензатори в електронни схеми. Част 2
Борис Аладишкин
Вижте също на i.electricianexp.com
: