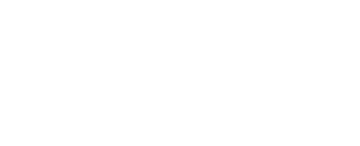Kategorijas: Piedāvātie raksti » Praktiskā elektronika
Skatījumu skaits: 124786
Komentāri par rakstu: 1
Osciloskopa mērīšanas veikšana
 Digitālais osciloskops, protams, ir daudz pilnīgāks nekā parastais elektroniskais, tas ļauj atcerēties viļņu formas, var izveidot savienojumu ar personālo datoru, tam ir matemātiska rezultātu apstrāde, ekrāna marķieri un vēl daudz vairāk. Bet, ņemot vērā visas priekšrocības, šīm jaunās paaudzes ierīcēm ir viens būtisks trūkums - tā ir augsta cena.
Digitālais osciloskops, protams, ir daudz pilnīgāks nekā parastais elektroniskais, tas ļauj atcerēties viļņu formas, var izveidot savienojumu ar personālo datoru, tam ir matemātiska rezultātu apstrāde, ekrāna marķieri un vēl daudz vairāk. Bet, ņemot vērā visas priekšrocības, šīm jaunās paaudzes ierīcēm ir viens būtisks trūkums - tā ir augsta cena.
Tieši viņa padara digitālo osciloskopu nepieejamu amatieru vajadzībām, kaut arī ir “kabatas” osciloskopi tikai dažu tūkstošu rubļu vērtībā, kas tiek pārdoti vietnē Aliexpress, taču tos izmantot nav īpaši ērti. Nu, tikai interesanta rotaļlieta. Tāpēc, kamēr mēs runāsim par mērījumiem, izmantojot elektronisko osciloskopu.
Par tēmu osciloskopa izvēlei lietošanai mājas laboratorijā internetā var atrast pietiekamu skaitu forumu. Nenoliedzot digitālo osciloskopu priekšrocības, daudzos forumos ieteicams izvēlēties vienkāršus, maza izmēra un uzticamus vietējos osciloskopus C1-73 un C1-101 un tamlīdzīgus, ar kuriem mēs iepriekš tikāmies šo rakstu.
Par diezgan pieņemamu cenu šīs ierīces ļaus veikt lielāko daļu radioamatieru uzdevumu. Pa to laiku iepazīsimies ar vispārējiem mērījumu principiem, izmantojot osciloskopu.

1. attēls. Osciloskops S1-73
Ko mēra osciloskops
Izmērītais signāls tiek padots uz vertikālā novirzes kanāla Y ieeju, kam ir liela ieejas pretestība, parasti 1MΩ, un maza ieejas kapacitāte, ne vairāk kā 40pF, kas ļauj izmērītajā signālā radīt minimālus traucējumus. Šie parametri bieži tiek norādīti blakus vertikālā novirzes kanāla ievadam.

2. attēls. Osciloskops C1-101
Augsta ieejas pretestība ir raksturīga voltmetriem, tāpēc var droši teikt, ka osciloskops mēra spriegumu. Ārējo ieejas dalītāju izmantošana ļauj samazināt ieejas kapacitāti un palielināt ieejas pretestību. Tas arī samazina osciloskopa ietekmi uz pētāmo signālu.
Jāatceras, ka ir speciāli augstfrekvences osciloskopi, kuru ieejas pretestība ir tikai 50 omi. Radioamatieru praksē šādas ierīces neatrod pielietojumu. Tāpēc turpmāk mēs pievērsīsim uzmanību parastie universālie osciloskopi.
Y kanāla joslas platums
Osciloskops mēra spriegumus ļoti plašā diapazonā: no līdzstrāvas spriegumiem līdz pietiekami augstas frekvences spriegumiem. Sprieguma svārstības var būt diezgan dažādas - no desmitiem milivoltu līdz desmitiem voltu, un, ja tiek izmantoti ārējie sadalītāji līdz vairākiem simtiem voltu.
Jāpatur prātā, ka vertikālās novirzes Y db kanāla joslas platums ne mazāk kā 5 reizes augstāka par mērāmā signāla frekvenci. Tas ir, vertikālās novirzes pastiprinātājam ir jāpārsniedz vismaz piektā pētāmā signāla harmonika. Tas ir īpaši nepieciešams, pētot taisnstūrveida impulsus, kuros ir daudz harmoniku, kā parādīts 3. attēlā. Tikai šajā gadījumā ekrānā tiek iegūts attēls ar minimāliem traucējumiem.
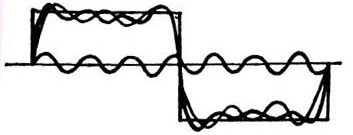
3. attēls. Taisnstūra signāla sintēze no harmoniskajiem komponentiem
Papildus pamata frekvencei 3. attēlā parādīta trešā un septītā harmonika. Palielinoties harmoniskajam skaitam, tā frekvence palielinās: trešās harmonikas frekvence ir trīs reizes augstāka nekā pamata, piektā harmonika ir piecas reizes, septītā ir septiņa utt. Attiecīgi samazinās augstāko harmoniku amplitūda: jo lielāks harmonisko skaitlis, jo mazāka ir tā amplitūda. Tikai tad, ja vertikālā kanāla pastiprinātājs bez lielas vājināšanas var palaist garām augstākās harmonikas, impulsa attēls būs taisnstūrveida.
4. attēlā parādīta līkuma līknes viļņu forma ar nepietiekamu Y kanāla joslas platumu.
4. attēls
Meandrs ar frekvenci 500 KHz izskatās kaut kas līdzīgs OMSh-3M osciloskopa ekrānā ar joslas platumu 0 ... 25 KHz. It kā taisnstūrveida impulsi tiktu izlaisti caur integrējošo RC ķēdi. Šādu osciloskopu ražoja padomju rūpniecība laboratorijas darbiem fizikas stundās skolās. Pat šīs ierīces barošanas spriegums drošības apsvērumu dēļ nebija 220, bet tikai 42V. Ir pilnīgi skaidrs, ka osciloskops ar šādu joslas platumu ļaus novērot signālu ar frekvenci ne vairāk kā 5 kHz, gandrīz nekropļojot.
Parastajam universālajam osciloskopam joslas platums visbiežāk ir 5 MHz. Pat ar šādu joslu jūs varat redzēt signālu līdz 10 MHz un augstāku, bet ekrānā saņemtais attēls ļauj spriest tikai par šī signāla esamību vai neesamību. Būs grūti pateikt kaut ko par tā formu, taču dažās situācijās forma nav tik svarīga: piemēram, ir sinusoidālais ģenerators, un pietiek tikai pārliecināties, vai šis sinusoīds ir vai nav. Tieši šāda situācija ir parādīta 4. attēlā.
Mūsdienu skaitļošanas sistēmas un sakaru līnijas darbojas ļoti augstās frekvencēs, pēc simtiem megahercu. Lai redzētu šādus augstas frekvences signālus, osciloskopa joslas platumam jābūt vismaz 500 MHz. Tik plaša josla patiešām “paplašina” osciloskopa cenu.
Piemērs ir digitālais osciloskops U1610A, kas nav parādīts 5. attēlā. Tās joslas platums ir 100 MHz, un cena ir gandrīz 200 000 rubļu. Piekrītu, ne visi var atļauties iegādāties tik dārgu ierīci.

5. attēls
Ļaujiet lasītājam neuzskatīt šo attēlu par sludinājumu, jo visas pārdevēja koordinātas nav nokrāsotas: jebkura līdzīga ekrānuzņēmums var parādīties šī attēla vietā.
Pētīto signālu veidi un to parametri
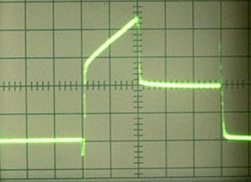
Dabā un tehnoloģijās visizplatītākais svārstību veids ir sinusoīds. Šī ir tā pati ilgstošās ciešanas funkcija Y = sinX, kas notika skolā trigonometrijas stundās. Diezgan daudziem elektriskiem un mehāniskiem procesiem ir sinusoidāla forma, lai gan elektroniskajā tehnoloģijā diezgan bieži tiek izmantoti citi signālu veidi. Daži no tiem ir parādīti 6. attēlā.
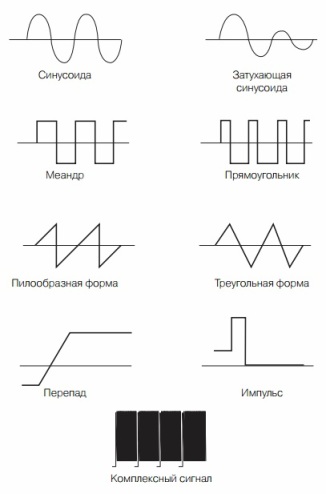
6. attēls. Elektrisko vibrāciju formas
Periodiski signāli. Signāla raksturojums
Universāls elektroniskais osciloskops ļauj precīzi pētīt periodiskos signālus. Ja, ieejot Y, jūs sūtāt reālu skaņas signālu, piemēram, mūzikas fonogrammu, tad ekrānā būs redzami nejauši mirgojoši pārrāvumi. Protams, nav iespējams detalizēti izpētīt šādu signālu. Šajā gadījumā palīdzēs izmantot digitālo atmiņas osciloskopu, kas ļauj saglabāt viļņu formu.
Svārstības, kas parādītas 6. attēlā, ir periodiskas, atkārtotas pēc noteikta laika T. T. To sīkāk var apsvērt 7. attēlā.
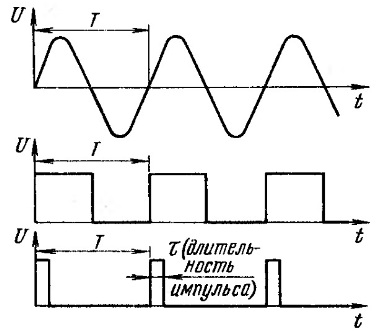
7. attēls. Periodiskas svārstības
Svārstības ir attēlotas divdimensiju koordinātu sistēmā: spriegumu mēra gar ordinātu asi, bet laiku mēra gar abscisas asi. Spriegumu mēra voltos, laiku sekundēs. Elektrisko vibrāciju laiku bieži mēra milisekundēs vai mikrosekundēs.
Papildus komponentiem X un Y, viļņu formā ir arī komponenta Z intensitāte vai vienkārši spilgtums (8. attēls). Tieši viņa ieslēdz gaismu uz priekšējās gaismas laiku un nodziest uz atpakaļgaitas laiku. Dažiem osciloskopiem ir ieeja spilgtuma kontrolei, ko sauc par ieeju Z. Ja šai ievadam pieliek impulsa spriegumu no atsauces ģeneratora, tad uz ekrāna var redzēt frekvences uzlīmes. Tas ļauj precīzāk izmērīt signāla ilgumu pa X asi.
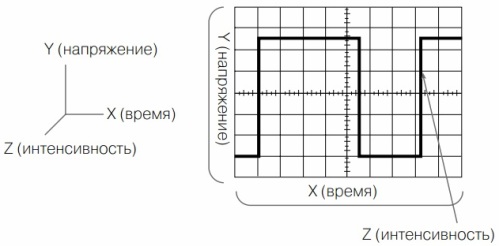
8. attēls. Trīs izmeklētā signāla komponenti
Mūsdienu osciloskopiem, kā likums, ir laika kalibrētas svārstības, kas ļauj precīzi noteikt laiku. Tāpēc, lai izveidotu tagus, nav nepieciešams izmantot ārēju ģeneratoru.
7. attēla augšpusē ir sinusoidāls vilnis. Ir viegli redzēt, ka tas sākas koordinātu sistēmas sākumā. Laikā T (periodā) tiek veikta viena pilnīga svārstība. Tad viss atkārtojas, nākamais periods. Šādus signālus sauc par periodiskiem.
Taisnstūra signāli ir parādīti zem sinusoidālā viļņa: meander un taisnstūra impulss. Tie ir arī periodiski ar T. periodu. Impulsa ilgumu apzīmē ar τ (tau). Lāpstiņrādītāja gadījumā impulsa ilgums τ ir vienāds ar pauzes ilgumu starp impulsiem, kas ir tikai puse no perioda T. Tāpēc meanderis ir taisnstūra signāla īpašs gadījums.
Pienākums un nodokļa likme
Taisnstūra impulsu raksturošanai tiek izmantots parametrs, ko sauc par darba ciklu. Šī ir impulsa atkārtošanās perioda T un impulsa ilguma τ attiecība. Lidmašīnai darba cikls ir vienāds ar diviem, - vērtība ir bez dimensijas: S = T / τ.
Angļu valodas terminoloģijā ir tieši pretēji. Tur impulsus raksturo darba cikls, impulsa ilguma attiecība pret darba cikla periodu: D = τ / T. Piepildījuma koeficientu izsaka %%. Tādējādi līkumam, D = 50%. Izrādās, ka D = 1 / S, darba cikls un darba cikls ir savstarpēji apgriezti, kaut arī tie raksturo vienu un to pašu impulsa parametru. Meandra viļņa forma ir parādīta 9. attēlā.
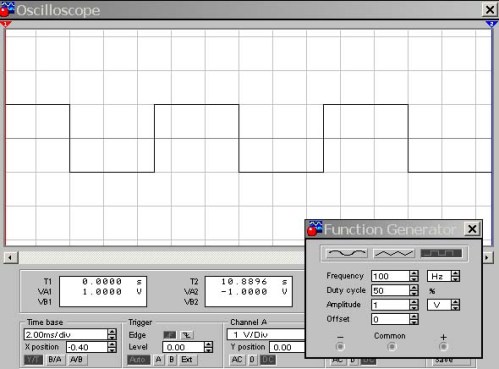
9. attēls. Meandra viļņa forma D = 50%
Šeit osciloskopa ieeja ir savienota ar funkcionālā ģeneratora izeju, kas uzreiz tiek parādīta attēla apakšējā stūrī. Un šeit uzmanīgs lasītājs var uzdot jautājumu: “1 V ģeneratora izejas signāla amplitūda, osciloskopa ieejas jutība ir 1 V / div., Un ekrāns parāda taisnstūra impulsus ar 2 V amplitūdu. Kāpēc?
Fakts ir tāds, ka funkcionālais ģenerators ģenerē bipolārus taisnstūrveida impulsus attiecībā pret 0V līmeni, aptuveni tāds pats kā sinusoīds, ar pozitīvu un negatīvu amplitūdu. Tāpēc osciloskopa ekrānā tiek novēroti impulsi ar diapazonu ± 1 V. Nākamajā attēlā mēs mainām darba ciklu, piemēram, uz 10%.
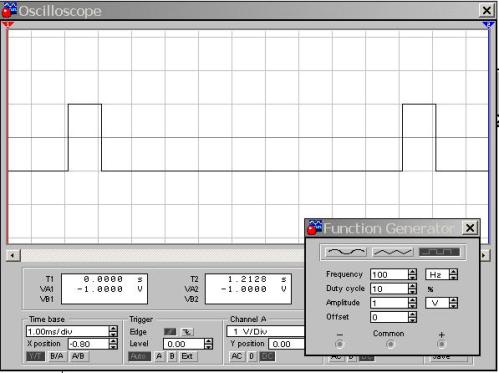
10. attēls. Taisnstūra impulss D = 10%
Ir viegli redzēt, ka impulsa atkārtošanās periods ir 10 šūnas, savukārt impulsa ilgums ir tikai viena šūna. Tāpēc D = 1/10 = 0,1 vai 10%, kā redzams no ģeneratora iestatījumiem. Ja darba cikla aprēķināšanai izmantojat formulu, iegūst S = T / τ = 10/1 = 1 - vērtība ir bezizmēra. Šeit mēs varam secināt, ka darba cikls impulsu raksturo daudz skaidrāk nekā darba cikls.
Faktiski pats signāls palika tāds pats kā 9. attēlā: taisnstūra impulss ar amplitūdu 1 V un frekvenci 100 Hz. Mainās tikai piepildījuma koeficients vai darba cikls, piemēram, kāds ir pazīstamāks un ērtāks. Bet 10. attēla novērošanas ērtībai skenēšanas ilgums ir samazināts uz pusi, salīdzinot ar 9. attēlu, un tas ir 1 ms / div. Tāpēc signāla periods ekrānā aizņem 10 šūnas, kas ļauj diezgan viegli pārbaudīt, vai darba cikls ir 10%. Izmantojot reālu osciloskopu, slaucīšanas ilgums tiek izvēlēts aptuveni tāds pats.
Taisnstūra impulsa sprieguma mērīšana
Kā minēts raksta sākumā, osciloskops mēra spriegumu, t.i. potenciālā starpība starp diviem punktiem. Parasti mērījumus veic attiecībā pret parastu vadu, zemējumu (nulles voltiem), lai gan tas nav nepieciešams. Principā ir iespējams izmērīt signāla vērtības no minimālās līdz maksimālajai (maksimālā vērtība, no maksimuma uz maksimumu). Jebkurā gadījumā mērīšanas darbības ir diezgan vienkāršas.
Taisnstūra impulsi visbiežāk ir vienpolāri, kas ir raksturīgi digitālajām tehnoloģijām. Kā izmērīt taisnstūra impulsa spriegumu, parādīts 11. attēlā.
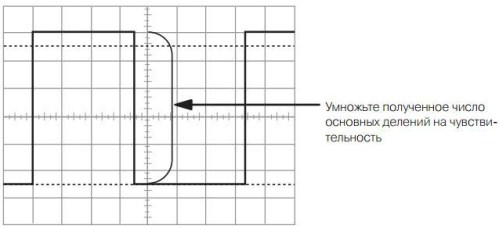
11. attēls. Taisnstūra impulsa amplitūdas mērīšana
Ja vertikālās novirzes kanāla jutība ir 1V / div, tad izrādās, ka attēlā redzams impulss ar 5,5 V spriegumu. Ar jutību 0,1V / div. Spriegums būs tikai 0,5 V, lai gan ekrānā abi impulsi izskatās tieši vienādi.
Ko vēl var redzēt taisnstūra impulsā
Taisnstūra impulsi, kas parādīti 9., 10. attēlā, ir vienkārši ideāli, jo tos sintezē Electronics WorkBench. Un impulsa frekvence ir tikai 100 Hz, tāpēc problēmas ar attēla "kvadrātu" nevar rasties. Reālā ierīcē ar lielu atkārtošanās ātrumu impulsi ir nedaudz izkropļoti, pirmkārt, uzstādīšanas induktivitātes dēļ parādās dažādi impulsi un pārrāvumi, kā parādīts 12. attēlā.
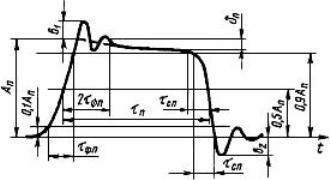
12. attēls. Īsts taisnstūra impulss
Ja jūs nepievēršat uzmanību šādiem "sīkumiem", tad taisnstūra impulss izskatās tāds, kā parādīts 13. attēlā.
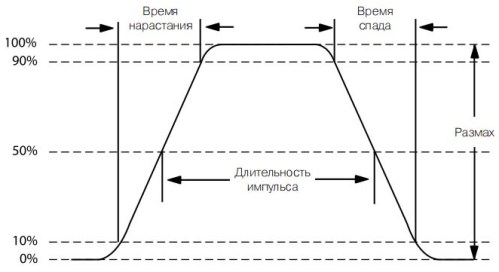
13. attēls. Taisnstūra impulsa parametri
Attēlā parādīts, ka impulsa vadošās un aizmugurējās malas neparādās uzreiz, bet tām ir zināms kāpuma un krituma laiks, un tās ir nedaudz slīpas attiecībā pret vertikālo līniju. Šis slīpums ir saistīts ar mikroshēmu un tranzistoru frekvences īpašībām: jo augstāks ir frekvences tranzistors, jo mazāk impulsu “frontes”. Tāpēc impulsa ilgumu nosaka 50% no visa diapazona līmeņa.
Tā paša iemesla dēļ impulsa amplitūdu nosaka ar līmeni 10 ... 90%. Impulsa ilgumu, kā arī spriegumu nosaka, horizontālās skalas dalījumu skaitu reizinot ar dalījuma vērtību, kā parādīts 14. attēlā.
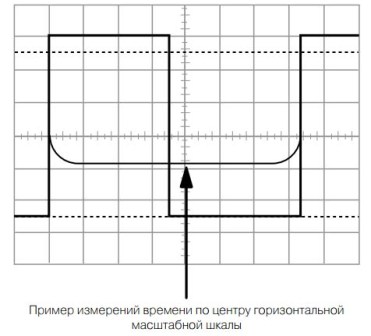
14. attēls.
Attēlā parādīts viens taisnstūra impulsa periods, kas nedaudz atšķiras no vidējā rādītāja: pozitīva impulsa ilgums ir 3,5 horizontālās skalas dalījumi, un pauzes ilgums ir 3,8 dalījumi. Pulsa atkārtošanās periods ir 7,3 dalījums. Šāds attēls var piederēt vairākiem dažādiem impulsiem ar dažādām frekvencēm. Viss būs atkarīgs no slaucīšanas ilguma.
Pieņemsim, ka skenēšanas ilgums ir 1ms / div. Tad impulsa atkārtošanās periods ir 7,3 * 1 = 7,3 ms, kas atbilst frekvencei F = 1 / T = 1 / 7,3 = 0,1428KHz vai 143 Hz. Ja skenēšanas ilgums ir 1 µs / div, tad frekvence izrādīsies tūkstoš reižu augstāka, proti, 143KHZ.
Izmantojot datus 14. attēlā, nav grūti aprēķināt impulsa darba ciklu: S = T / τ = 7,3 / 3,5 = 2,0857, tas izrādās gandrīz kā līkumu līkne. Darba cikla darba cikls D = τ / T = 3,5 / 7,3 = 0,479 vai 47,9%. Jāatzīmē, ka šie parametri nekādā ziņā nav atkarīgi no frekvences: darba ciklu un darba ciklu aprēķināja, vienkārši sadalot viļņu formā.
Ar taisnstūrveida impulsiem viss šķiet skaidrs un vienkāršs. Bet mēs pilnībā aizmirsām par sinusoidālo vilni. Faktiski tas pats ir tur: jūs varat izmērīt spriegumus un laika parametrus. Viens sinusa viļņa periods ir parādīts 15. attēlā.
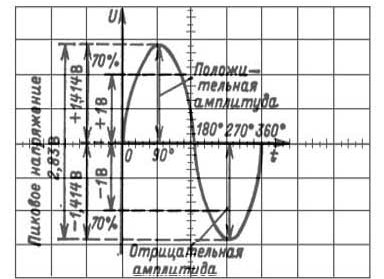
15. attēls. Sinusoidālā viļņa parametri
Acīmredzot attēlā redzamajam sinusoidam vertikālās novirzes kanāla jutība ir 0,5 V / div. Atlikušos parametrus var viegli noteikt, dalījumu skaitu reizinot ar 0.5V / div.
Sinusoidālais vilnis var būt vēl viens, kas būs jāmēra ar jutīgumu, piemēram, 5 V / div. Tad 1 V vietā jūs iegūstat 10 V. Tomēr ekrānā abu sinusoīdu attēls izskatās tieši tāds pats.
Parādītā sinusoīda laiks nav zināms. Ja pieņemsim, ka skenēšanas ilgums ir 5ms / div, periods būs 20ms, kas atbilst 50Hz frekvencei. Skaitļi grādos uz laika ass norāda sinusoīda fāzi, kaut arī tas nav īpaši svarīgi atsevišķam sinusoidam. Biežāk ir jānosaka fāzes nobīde (tieši milisekundēs vai mikrosekundēs) vismaz starp diviem signāliem. Vislabāk to izdarīt ar divu staru osciloskopu. Kā tas tiek darīts, tiks parādīts zemāk.
Kā izmērīt strāvu ar osciloskopu
Dažos gadījumos ir nepieciešams izmērīt strāvas lielumu un formu. Piemēram, maiņstrāva, kas plūst caur kondensatoru, pārsniedz spriegumu par ¼ perioda. Tad atvērtā ķēdē tiek iekļauts rezistors ar nelielu pretestību (omi desmitdaļas). Šāda pretestība neietekmē ķēdes darbību. Sprieguma kritums visā šajā rezistorā parādīs strāvas formu un lielumu, kas plūst caur kondensatoru.
Aptuveni tādā pašā veidā ir izkārtots līdzīgs manometrs ar mērierīci, kas tiks iekļauts elektriskās ķēdes pārtraukumā. Šajā gadījumā mērīšanas rezistors atrodas pašā ampērmetrā.
Ķēde strāvas mērīšanai caur kondensatoru ir parādīta 16. attēlā.
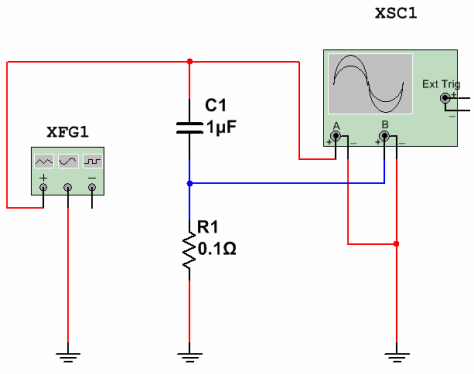
16. attēls. Strāvas mērīšana caur kondensatoru
Sinusoidālais spriegums 50 Hz ar 220 V amplitūdu no XFG1 ģeneratora (sarkans stars uz osciloskopa ekrāna) tiek piegādāts seriālajai shēmai no kondensatora C1 un mērīšanas rezistora R1. Sprieguma kritums visā šajā rezistorā parādīs strāvas formu, fāzi un lielumu caur kondensatoru (zilo staru). Kā tas izskatīsies osciloskopa ekrānā, parādīts 17. attēlā.
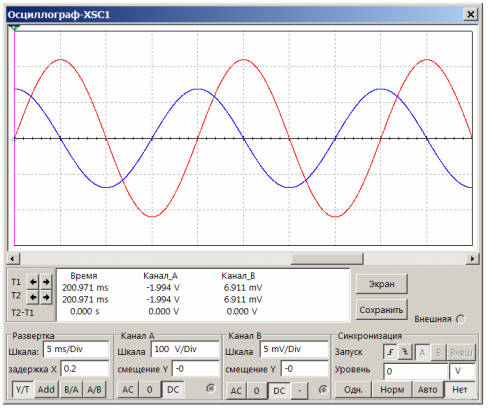
17. attēls. Strāva caur kondensatoru pārsniedz spriegumu par ¼ perioda
Pie sinusoidālā viļņa frekvences 50 Hz un skenēšanas laika 5 ms / Div vienā sinusa viļņa periodā notiek 4 dalījumi pa X asi, kas ir ļoti ērti novērošanai. Ir viegli redzēt, ka zilais stars ir priekšā sarkanajam tieši par 1 dalījumu pa X asi, kas atbilst ¼ no perioda. Citiem vārdiem sakot, strāva caur kondensatoru pārsniedz fāzes spriegumu, kas pilnībā atbilst teorijai.
Lai aprēķinātu strāvu caur kondensatoru, pietiek ar Ohma likumu: I = U / R. Ja mērīšanas rezistora pretestība ir 0,1 omi, sprieguma kritums tam ir 7 mV. Šī ir amplitūdas vērtība. Tad maksimālā strāva caur kondensatoru būs 7 / 0,1 = 70mA.
Strāvas formas mērīšana caur kondensatoru nav ļoti steidzams uzdevums, viss ir skaidrs un bez mērījumiem. Kondensatora vietā var būt jebkura slodze: induktors, motora tinumu, tranzistora pastiprinātāja pakāpi un daudz ko citu. Ir svarīgi, lai šo metodi varētu izmantot strāvas izpētei, kas dažos gadījumos pēc formas ievērojami atšķiras no sprieguma.
Boriss Aladyshkin
Skatīt arī vietnē i.electricianexp.com
: