Būla algebra. 1. daļa. Nedaudz vēstures

Skolā mēs visi studējām algebru, bet viņi tur nerunāja par Būla algebru. Kāda ir atšķirība starp Boolean algebra un skolas algebra, tās parādīšanās vēsture, problēmas un lietojumi ir aprakstīti šajā rakstā.

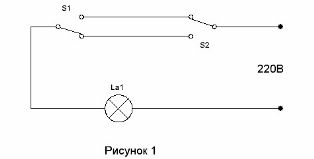
Ķēde, kas ļauj diviem slēdžiem ieslēgt gaismu koridorā pie koridora ieejas un izslēgt to, ieejot telpā, bija zināma jau ļoti ilgu laiku (sk. Koridora apgaismojuma vadības shēma) Tas parādīts 1. attēlā.

1. uzdevums. Sarežģītāk. Izveidojiet diagrammu, kas ļauj ieslēgt un izslēgt apgaismojumu telpā ar jebkuru no 3 dažādiem slēdžiem. Slēdži atrodas pie istabas ieejas, virs gultas un pie rakstāmgalda.

2. uzdevums.

Sporta komitejā, piemēram, rūpnīcas komitejā, pulcējās 5 tiesneši.

Katram no viņiem jābalso par atšķirīgiem lēmumiem. Lēmumu pieņem ar balsu vairākumu, bet tikai ar papildu nosacījumu, ka par to balso komitejas priekšsēdētājs.

Tiesneši balso, nospiežot pogu, kas aizver slēdzi, kas atrodas zem galda, pie kura viņi sēž. Noslēdzot slēdzi, viņi balso par, atvienojot mīnusus. Uzzīmējiet vienkāršu diagrammu, kas ļauj automātiski redzēt balsošanas rezultātus. Vienkāršākā gadījumā vienkārši ar iedegtu spuldzi - lēmums tika pieņemts, nedeg - nē.

3. uzdevums. Praksē tas ir maz ticams, bet kā sarežģīts izglītības uzdevums ir diezgan piemērots.

Lielā sešstūra telpā uz katras sienas ir uzstādīts viens slēdzis. Izveidojiet ķēdi tā, lai jebkurā laikā jūs varētu ieslēgt vai izslēgt gaismu telpā, pagriežot vienu (jebkuru) slēdzi.

Pēc tam, kad trīs līdz četras dienas esat neveiksmīgi sēdējis virs uzdevumiem, īslaicīgi atlieciet tos malā. Un aizņemties Būla algebra. Tā ir Būla algebra vai, kā to sauc arī Būla algebra, releja ķēdes algebra, palīdzēs jums atrisināt jūsu problēmas.

Kas ir Būla algebra?

Savādi, neskatoties uz to, ka piecus gadus viņi skolā mācījās algebru, daudzi studenti un vēlāk arī pieaugušie nespēs atbildēt uz jautājumu, kas ir algebra? Algebra ir zinātne, kas pēta dažu elementu kopas un darbības uz tiem.

Skolas kursā algebrā šādi elementi ir skaitļi. Ciparus var apzīmēt nevis ar cipariem, bet ar burtiem, visi to zina. Pirmajās algebras stundās tas daudziem skolēniem vienmēr sagādā grūtības. Atcerieties, cik grūti sākumā bija pierast pie burtu locīšanas, nevis skaitļiem, risināt vienādojumus, kas neko neteica.

Droši vien katrs no mums pēc tam uzdeva sev jautājumu: “Kāpēc mums ciparu vietā jāievada burti, un vai tas vispār ir vajadzīgs?” Un tikai vēlāk jūs redzējāt, kādas priekšrocības algebra dod, risinot problēmas, salīdzinot ar aritmētiku.

Algebra tiek izmantota daudzās eksaktajās zinātnēs. Tā ir fizika, mehānika, sopromāts, elektrība. Ohmas likums nav nekas vairāk kā algebrisks vienādojums: pietiek ar burtu vietā aizstāt to skaitliskās vērtības, lai uzzinātu, kāda strāva plūdīs slodzē, vai kāda pretestība ir kādas shēmas sadaļai.

Tātad jūs iepazināmies ar skaitļu algebru vai ar elementāru algebru. Galvenais un gandrīz unikālais uzdevums ir iegūt atbildi uz jautājumu: “Ar ko X ir vienāds? Cik daudz? ”

Vidusskolā viņi pēta vektora algebras pirmsākumus. Šī algebra būtiski atšķiras no elementārās algebras. Tam ir atšķirīgs izpētītā kopuma un citu darbības noteikumu raksturs. Atrisinot vektora vienādojumu, atbildē iegūstam vektoru, kas nav parasts skaitlis un kas atbild uz jautājumu “Cik daudz?”

Vektora algebras formulas daudzos aspektos atšķiras no elementārās algebras formulām. Piemēram, elementārajā algebrā un vektora algebrā ir pievienotā darbība. Bet tas tiek veikts pavisam citādos veidos.Skaitļu pievienošana nepavisam neatšķiras no vektoru pievienošanas.

Ir arī citas algebras: lineārā algebra, struktūru algebra, gredzenu algebra, loģikas algebra vai, kas ir tas pats, Būla algebra. Jūs, iespējams, skolas stundās nedzirdējāt vārdu. Džordžs Būls - bet visi zina vienas no talantīgajām meitām Ethel Voinich (1864 - 1960) vārdu. Viņa sarakstīja romānu "Gadfly", kas stāsta par cīņu par Itālijas karboniešu tiesībām.

Džordžs Bulls dzimis Anglijā 1815. gada 2. novembrī. Visu mūžu viņš skolā strādāja par matemātikas un fizikas skolotāju. No viņa studentu memuāriem ir zināms, cik lielu nozīmi Bols piešķīra studentu radošo spēju attīstībai. Prezentējot jaunu materiālu, viņš centās pārliecināties, ka viņa studenti paši “no jauna atklāja” noteiktas formulas un likumus.

Stāstot studentiem par grūtībām, ar kurām zinātnieki neizbēgami saskārās, meklējot patiesību, skolotājam patika atkārtot vienu austrumu gudrību: pat Persijas tronis nevar sagādāt cilvēkam tik lielu prieku kā mazākais zinātniskais atklājums. Buhls nekad nav zaudējis cerību, ka kādreiz viņa studenti veiks patiesu atklājumu.

Buhla zinātnisko interešu loks bija ļoti plašs: viņu vienlīdz interesēja matemātika un loģika - likumu zinātne un domāšanas formas. Tajos laikos loģika tika uzskatīta par humanitāro zinātni, un daudzi, kas zināja Džordžu Būlu, bija pārsteigti par to, kā precīzas izziņas metodes, kas raksturīgas matemātikai, un tīri aprakstošas ​​loģikas metodes varētu pastāvēt līdzās vienai personai.

Bet zinātnieks gribēja padarīt likumu zinātni un domāšanas formas tikpat stingras kā jebkura no dabaszinātnēm, teiksim, matemātika un fizika. Par to Boule sāka apzīmēt nevis ciparus kā burtus, kā tas tiek darīts parastajā algebrā, bet gan apgalvojumus, un parādīja, ka šādi vienādojumi, kas ir ļoti līdzīgi algebriskajiem, var atrisināt jautājumus par cilvēka izteikto apgalvojumu patiesumu un nepatiesību. Tātad radās Būla algebra.

Bet ilgi pirms Džordža Bula vācu matemātiķis un filozofs Gotfrīds Leibnizs (1646-1716) pirmo reizi nāca klajā ar ideju izveidot zinātni, kas apzīmētu visus parastās sarunvalodas runas jēdzienus ar simboliem un izveidotu kādu jaunu algebru šo simbolu apvienošanai.

Pēc šādas zinātnes radīšanas, pēc Leibnica domām, zinātnieki un filozofi pārstās strīdēties un kliegt viens otram, uzzināt patiesību, bet viņi paņems zīmuli un mierīgi pateiks: “Aprēķināsim!”

Mūsdienās loģikas algebra ir kļuvusi par būtisku matemātikas sastāvdaļu. Viens no tās uzdevumiem ir atrisināt visa veida vienādojumus, kuru skaitliskās attiecības tiek aizstātas ar alfabētiskām. Katrs no jums, iespējams, visas dzīves garumā atcerējās, kā ar burtu koeficientiem atrisināt otrās un trešās pakāpes vienādojumus. Tātad, Boole savā jaunajā algebrā izmantoja visas šīs formulas un noteikumus.

Būla algebrā jaunums ir tas, ka tajā pētītie kopas elementi nav skaitļi, bet gan paziņojumi. Ja, risinot parastos algebriskos vienādojumus, tiek noteikts, kāds skaitlis ir vienāds ar nezināmo X, skolas algebra meklē atbildi uz jautājumu: “Cik daudz?”

Loģikas algebra meklē atbildi uz jautājumu: “Vai šis vai tas apgalvojums ir apzīmēts ar burtu X?”

Paziņojuma jēgai un saturam šeit nav nozīmes. Katrs apgalvojums var būt tikai patiess vai nepatiess. Tas nevar būt daļēji patiess un daļēji nepatiess. Kā piemēru mēs varam atcerēties lozēšanas ar monētu.

Tajā tiek apskatīti tikai divi monētu stāvokļi - galvas vai astes. Pēc pušu vienošanās ērglis ir JĀ, un astes NĒ. Varbūtību teorijā citi starppunkti netiek ņemti vērā, kaut arī tie ir iespējami. Apgriezta monēta var nokrist uz malu, nokrist pa grīdu līdz krēsla vai galda kājām un palikt vertikālā stāvoklī vai pat iekrist plašā grīdas spraugā. (Pēc analoģijas ar elektriskajām ķēdēm pēdējās divas situācijas var uzskatīt par darbības traucējumiem sadeguša kontakta formā).Bet tajos laikos Būla algebra, diemžēl, nebija plaši izmantota.

Klods Šenons atkal “atklāja” Buhla algebru. 1938. gadā, vēl studējot Masačūsetsas Tehnoloģiju institūtā un Amerikā, jaunais Klods pierādīja, ka Būla algebra ir pilnīgi piemērota releju un komutācijas ķēžu analīzei un sintēzei.

Ar Būla algebras palīdzību ir ļoti viegli izveidot automātu, kas darbojas ar releju.Šim nolūkam, izrādās, jums precīzi jāzina, kas tieši mašīnai jādara, tas ir, jums ir jābūt tā darbības algoritmam. Tātad tika likts pamats digitālo mašīnu teorijai, kas darbojas pēc JĀ vai NĒ principa.

Tāda, īsi sakot, ir Būla algebras vēsture. Turpmākajos rakstos mēs apskatīsim tā pamatlikumus, kontaktu shēmu piemērus, kas ievieš šos likumus. Apsveriet to uzdevumu risinājumu, kuri tika doti raksta sākumā.

Raksta turpinājums: Būla algebra. 2. daļa. Pamatlikumi un funkcijas

Boriss Aladyshkin